Open-ended Questions

Syfte

Open-ended questions (OEQ) är utmanande för alla oavsett nivå och de kan individualisera undervisningen. De ger alla elever möjlighet att utveckla sin matematiska förmåga på sin nivå. En open-ended question innebär att eleverna arbetar både individuellt och i grupp. De lär av varandra, dels under det laborativa arbetet, men framför allt vid redovisningen som läraren håller i. En OEQ ger eleverna möjlighet att arbeta och tänka matematiskt. En OEQ skiljer sig från en öppen fråga därför att den också är ended! Ended betyder att det finns en gräns för vad som är rimligt.

Läraren reflekterar

I matte ”är” av tradition alla svar rätt eller fel och eleverna besvarar många frågor i alla möjliga kontexter som de kanske inte alls känner till. Vilken blir deras uppfattning av matematik? Hur får vi eleverna att reflektera? Hur får vi dem att förstå att de redan besitter viktiga kunskaper? Hur får vi dem att använda sina kunskaper i stället för att höra dem säga ”Det har vi redan gjort!”

Matematik är tyvärr för många elever att räkna i en bok – helst så fort som möjligt, helst fler sidor än kamraterna. Därför kan det vara svårt att bryta en (o)vana, i synnerhet som somliga elever inte tycks ha någon annan sporre än att komma längst fram i boken. Hur bryter man ovanor?

Att starta sin undervisning i en open-ended question innebär att man har stoff för åtskilliga lektioner framåt. Hur man går vidare utifrån utgångsfrågan beror på vilket mål man har med sin undervisning. Frågeställningen i kombination med lärarens matematikkunskaper ger elever i alla årskurser att utveckla sin matematik och lära sig mer utifrån vad man redan kan. OEQ kan kanske vara en möjlighet att utveckla såväl elevernas matematik som lärares matematikundervisning i alla årskurser.

Metod – Exempel på OEQ

Jämför ett typiskt läroboksexempel och en open-ended question:

• Hur mycket är 4 x 6?
• Berätta en liten historia om Ivan – vad som helst – och säg sen att en gång när han multiplicerade fick han svaret 24. Vad kan han ha multiplicerat?

Den första uppgiften har ett enda rätt svar och den lyckas i liten utsträckning att involvera eleverna. Den inbjuder i ringa omfattning till självständigt tänkande och det egna ansvaret är minimalt. Många elever gör inte sällan sina problem till lärarens och det blir lärarens problem att ”hjälpa” eleven till det rätta svaret om de själva inte lyckas. Den andra uppgiften ger alla elever möjligheter att tänka självständigt. Även den elev som gör det enkelt för sig ”lyckas”. Andra elever ser fler möjligheter och lämnar flera svar – en strategisk behandling av alla svar ger större möjlighet att hitta samband och mönster.

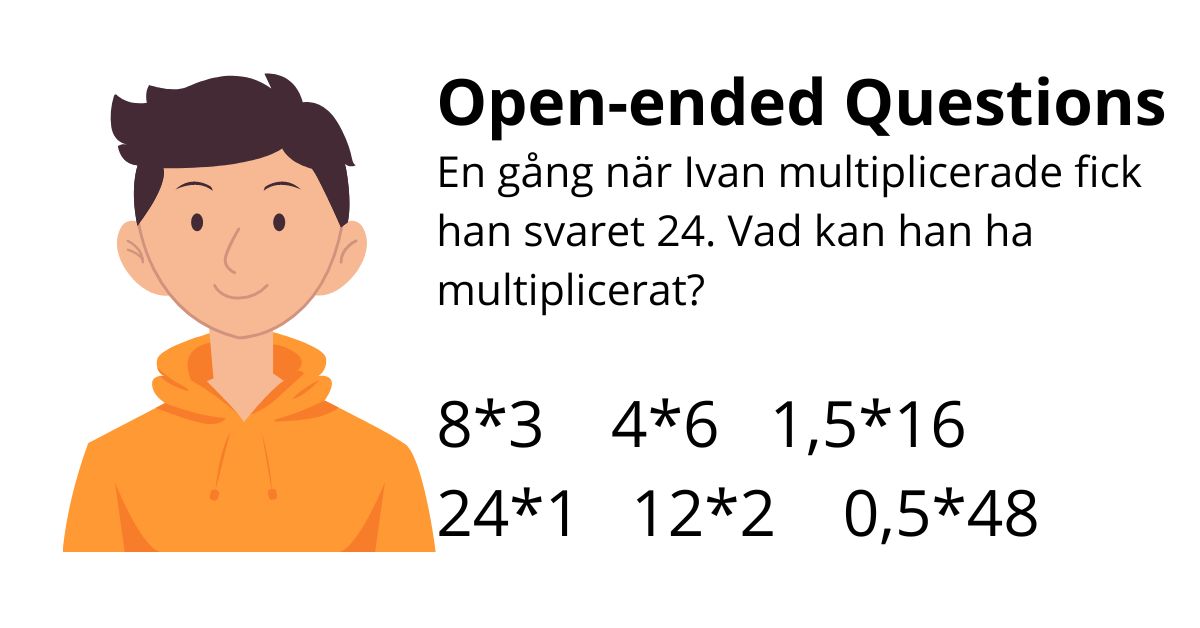
Uppgiften kan ta en hel lektion. Varje elev börjar på egen hand för att sedan jämföra med sina kamrater i gruppen och fortsätta leta efter nya infallsvinklar. Efter några minuters räknande tar läraren upp elevernas svar till diskussion, till exempel 3×8 och 1,5×16 och 0,5×48 och 0,25 x 96. Diskussionen om hur eleverna har tänkt kan fortsätta. Eleverna upptäcker då mångfalden av möjliga svar.

Nästa fråga kan vara: Lisa räknade och fick svaret 42. Vad kan hon ha multiplicerat? Förhoppningsvis kan vi se ett tydligt lärande då eleverna väljer multiplikationer av typen 84×0,5 och 168×0,25 och många andra alternativ.

Lgr22 Syfte

Utveckla taluppfattningen och förmåga att formulera och lösa problem med hjälp av matematik och värdera valda strategier.
Förmåga att föra och följa matematiska resonemang.

Centralt innehåll*

Formulering av matematiska frågeställningar utifrån vardagliga situationer.
Strategier för att lösa matematiska problem i elevnära situationer.

Kunskapskrav*

Eleven löser komplexa problem. Eleven ger förslag på alternativa tillvägagångssätt och värderar resultatens rimlighet. Eleven för och följer matematiska resonemang genom att framföra och bemöta påståenden med väl underbyggda matematiska argument. Eleven redogör för och samtalar om tillvägagångssätt på ett ändamålsenligt och effektivt sätt och använder då symboler och andra matematiska uttrycksformer.

* årskurs 4-6