Ett diagram utan siffror

Syfte

Träna på begrepp kring statistik och diagram, men också principer för att läsa diagram och ta reda på och sortera information av olika slag vilket idag blir allt viktigare.

Mina reflektioner

Normalt kanske läraren ställer mer eller mindre kluriga frågor utifrån diagrammet där all information redan finns, men här fick eleverna själva vara med i framtagandet av frågor. Eleverna förstod syftet med uppgiften, fick en koppling mellan matematikundervisningen och verkligheten och fick utöver det arbeta på sin nivå då uppgiften stimulerar till olika utmaningar för olika elever. Att lära tillsammans, med och av varandra är en annan sak som blev framträdande.

Förberedelser

Jag hade förberett en lektion kring diagram och tagit hjälp av ett diagram från SCB om folkmängd genom åren. Jag försökte att involvera eleverna i själva skapandet av uppgiften också (vad är eleverna intresserade av) genom att skala bort information som i traditionell undervisning kanske skulle ha serverats till eleverna redan inledningsvis. Jämför de två diagrammen nedan. Skillnaden i hur eleverna behöver involveras i arbetet kring de olika diagrammen syns tydligt.

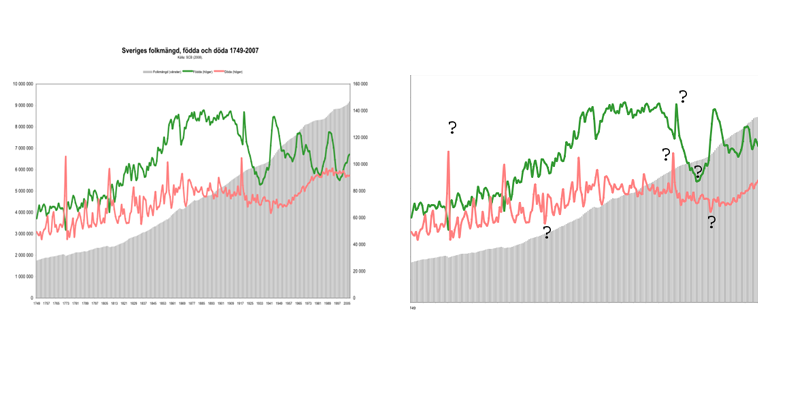
Metod och arbetsuppgifter

Jag inledde lektionen med diagrammet till höger där jag tagit bort i princip alla sifferuppgifter och information till diagrammet. Eleverna tittade under en minut på diagrammet och funderade över vad de tänkte när de såg bilden. Sedan fick de presentera sina funderingar i klassen. Eleverna förklarade vad diagrammet eventuellt kunde visa och gav motiveringar till detta. Några bad om information (som återfinns i det ”riktiga” diagrammet) vilket tyder på förståelse av vad ett linje/ stapeldiagram är. Andra diskuterade till exempel linjernas höjd och dess dalar och motiverade i stil med att diagrammet kanske hade med befolkning att göra, att dalarna berodde på krig, att linjerna representerade män och kvinnor respektive olika länder eller att staplarna var antal barn. Ytterligare elever diskuterade olika antal och något jag noterade var att eleverna direkt antog att antal skulle läsas av på y-axeln på detta diagram.

Att jobba vidare

När elevernas diskussioner klingat ut var de flesta överens om att diagrammet visade antal av något under en viss tid. Många hade alltså tolkat diagrammet rätt utan tillgång till all information. Sedan klickade jag in olika information efterhand (jag hade gjort en PowerPoint) och vi diskuterade vad just den informationen tillförde diagrammet. Vi hann också diskutera vad ”glappet” mellan de olika linjerna i diagrammet kunde innebära/ge oss för information och här visade några eleverna goda kunskaper kring problemlösning på temat statistik, befolkningsökning/minskning. Att sedan koppla årtal till historiska händelser vi läst om gav eleverna ytterligare en dimension kring hur data kan användas i andras yrkesliv eller i medier. Lektionen byggde jag kring följande frågor:

• Vad tänker du när du ser diagrammet?
• Vilken information behöver du för att förstå diagrammet?
• Vad hjälper diagrammet dig med?
• Vilken hjälp skulle diagrammet kunna ge andra?
• Finns det andra sätt att presentera informationen i diagrammet?

Lgr22 Syfte

Utveckla förmåga att formulera och lösa problem med hjälp av matematik och värdera valda strategier.
Förmåga att föra och följa matematiska resonemang.
Förmåga att använda matematikens uttrycksformer för att samtala om och redogöra för frågeställningar, beräkningar och slutsatser.

Centralt innehåll*

Tabeller och diagram för att beskriva resultat från undersökningar, såväl med som utan digitala verktyg. Tolkning av data i tabeller och diagram.
Formulering av matematiska frågeställningar utifrån vardagliga situationer.

Betygskriterier*

Eleven visar mycket goda kunskaper om matematiska begrepp samt använder och beskriver begrepp och samband mellan begrepp inom områdena taluppfattning och tals användning, algebra, geometri, sannolikhet och statistik samt samband och förändring med mycket god säkerhet.

Eleven väljer och använder ändamålsenliga och effektiva matematiska metoder för att göra beräkningar och lösa rutinuppgifter inom områdena taluppfattning och tals användning,  algebra, geometri, sannolikhet och statistik samt samband och förändring med mycket god säkerhet.

Eleven löser komplexa problem. Eleven ger förslag på alternativa tillvägagångssätt. I samband med problemlösning formulerar eleven enkla matematiska modeller som kan tillämpas i sammanhanget. Eleven värderar strategier och resultatens rimlighet på ett välutvecklat sätt.

* årskurs 4-6