Årskurs 7-9
Matematik
Föregående tips Nästa tipsTrafikflöden
Syfte
I temat kring sannolikhet, statistik och kombinatorik ska eleverna samla in och presentera/analysera och jämföra data i olika representationer kopplat till statistik.
Läraren reflekterar
Det finns kopplingar från detta till bland annat geografiämnet där eleverna ska utvecklas i att läsa av och tolka kartor och andra geografiska källor.
Metod
Eleverna gör en undersökning av trafikflöden under en del av lektion. Jag förbereder följande dokument till eleverna som kommer arbeta 2-2 eller 3-3 med uppgiften fast med några olika vägar under en 45-minuterslektion:
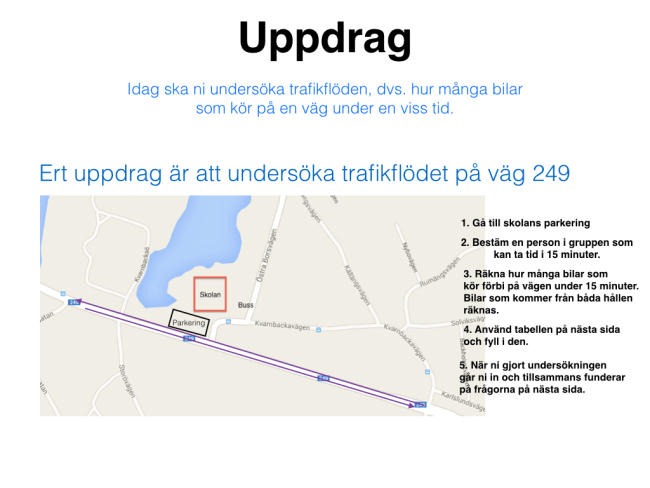
Elevprotokoll och frågor att fundera på:

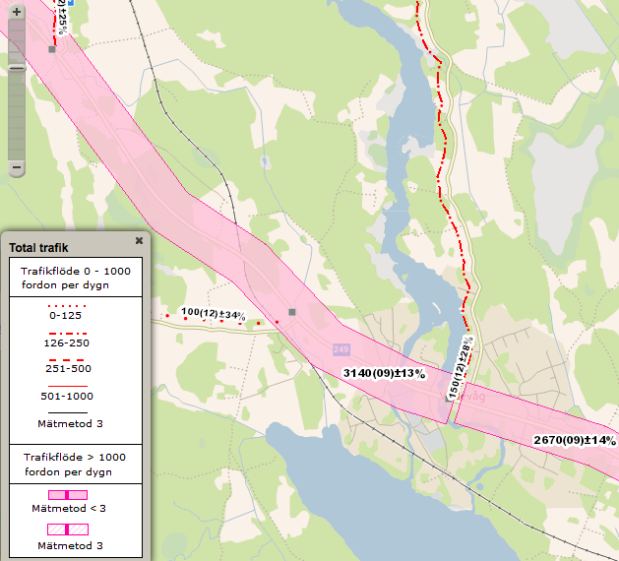
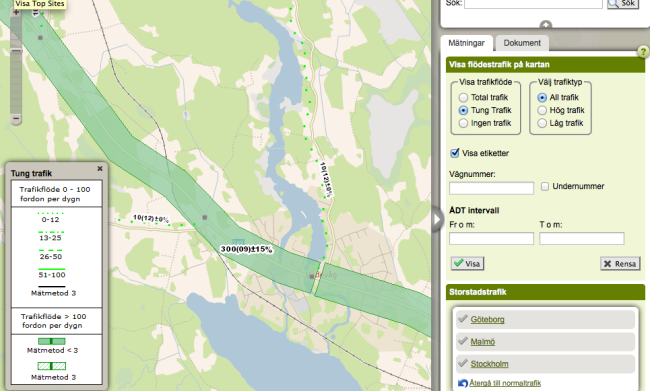
Nästa lektion jämför eleverna sina siffror med siffrorna trafikverket hade 2009. Jag hittade statistik på både tunga och lätta fordon på trafikverket från några år tillbaka då den senaste mätningen av flödena på tre av gatorna nära skolan gjorts. Så här kan de bilderna se ut:
Det är intressant att höra elevernas resonemang kring hur statistiken ska tolkas och vilken feedback ger varandra. Exempel på frågor som eleverna pratar om:
- Spelar tiden på dygnet någon roll för resultatet av deras mätning?
- Var kör flest lastbilar och varför?
- Var det tunga eller lätta fordon som var vanligast förekommande i mätningen. Varför?
- Hur skulle trafikverket genomföra mätningen för att den ska visa dem det som är avsett?
- Vad mätte vi egentligen genom vår undersökning?
- Vilka fler frågor har eleverna?
Förslag på fortsättning
Eleverna ska få möjlighet att presentera sin statistik i fina tabeller och diagram som de själva ska få tillverka med hjälp av surfplattor och datorer, ge respons/feedback på varandras skapelser och utveckla såväl förmågan att använda begrepp, att använda metoder för att lösa rutinuppgifter och inte minst att använda matematikens uttrycksformer och argumentera/förklara sina slutsatser.
Lärarens tankar om upplägget
Jag tror att när man inleder med en undersökning som eleverna själva får göra utan så mycket inblandning av mig kan en bra grund för hela arbetet kring temat läggas. Eleverna ska vidare efter detta få göra enkla undersökningar inom sannolikhetslära och att nyligen ha tränat på att dokumentera i tabeller och diagram kommer gynna eleverna vid dessa lektioner.
Lgr22 Syfte
Utveckla förmåga att använda och beskriva matematiska begrepp och samband mellan begrepp.
Förmåga att välja och använda lämpliga matematiska metoder för att göra beräkningar och lösa rutinuppgifter.
Förmåga att formulera och lösa problem med hjälp av matematik och värdera valda strategier.
Förmåga att föra och följa matematiska resonemang.
Förmåga att använda matematikens uttrycksformer för att samtala om och redogöra för frågeställningar, beräkningar och slutsatser.
Centralt innehåll*
Tabeller och diagram för att beskriva resultat från undersökningar, såväl med som utan digitala verktyg. Tolkning av data i tabeller och diagram.
Strategier för att lösa matematiska problem i elevnära situationer.
Formulering av matematiska frågeställningar utifrån vardagliga situationer.
Betygskriterier*
Eleven väljer och använder ändamålsenliga och effektiva matematiska metoder för att göra beräkningar och lösa rutinuppgifter inom områdena taluppfattning och tals användning, algebra, geometri, sannolikhet och statistik samt samband och förändring med mycket god säkerhet.
Eleven löser komplexa problem. Eleven ger förslag på alternativa tillvägagångssätt och värderar resultatens rimlighet.
Eleven för och följer matematiska resonemang genom att framföra och bemöta påståenden med väl underbyggda matematiska argument.
Eleven redogör för och samtalar om tillvägagångssätt på ett ändamålsenligt och effektivt sätt och använder då symboler och andra matematiska uttrycksformer.
* årskurs 4-6

Kommentarer