Årskurs 4-6
Matematik
Föregående tips Nästa tipsMultiplikationsbingo
Syfte
För att få en bild över elevernas kunskaper om multiplikationstabellen och deras förmåga att resonera, men också för att öva får eleverna spela multiplikationsbingo.
Läraren reflekterar om förutsättningarna
Eleverna har givetvis redan under tidigare år stött på begreppen multiplikation och division. De flesta har således en viss förförståelse för vad det innebär. Eleverna behöver förstå hur det går till att spela bingo.
Metod och uppgift
Eleverna fick själva rita upp varsin spelplan med 5×5 rutor. Därefter bad jag eleverna skriva in tal mellan 1 och 36 i rutorna, olika tal i samtliga rutor. Jag gick under tiden runt till några elever och frågade hur många rutor de hade att skriva in tal i för att se om de reflekterade över multiplikationen 5×5 eller om de helt enkelt räknade sina rutor en efter en.
Därefter tog jag fram två tärningar och frågade eleverna om de hade någon aning om varför jag ville att det högsta talet de skulle skriva in var talet 36? Någon elev gissade visserligen att det var min ålder men så delgav en elev resten av gruppen, med tärningarna som ledtråd, att sex multiplicerat med sex är lika med 36. När det var klarlagt hade alla förstått att vi skulle multiplicera den ena tärningens prickar med den andra. Produkten skulle kryssas för om den fanns i någon av de 25 rutorna.
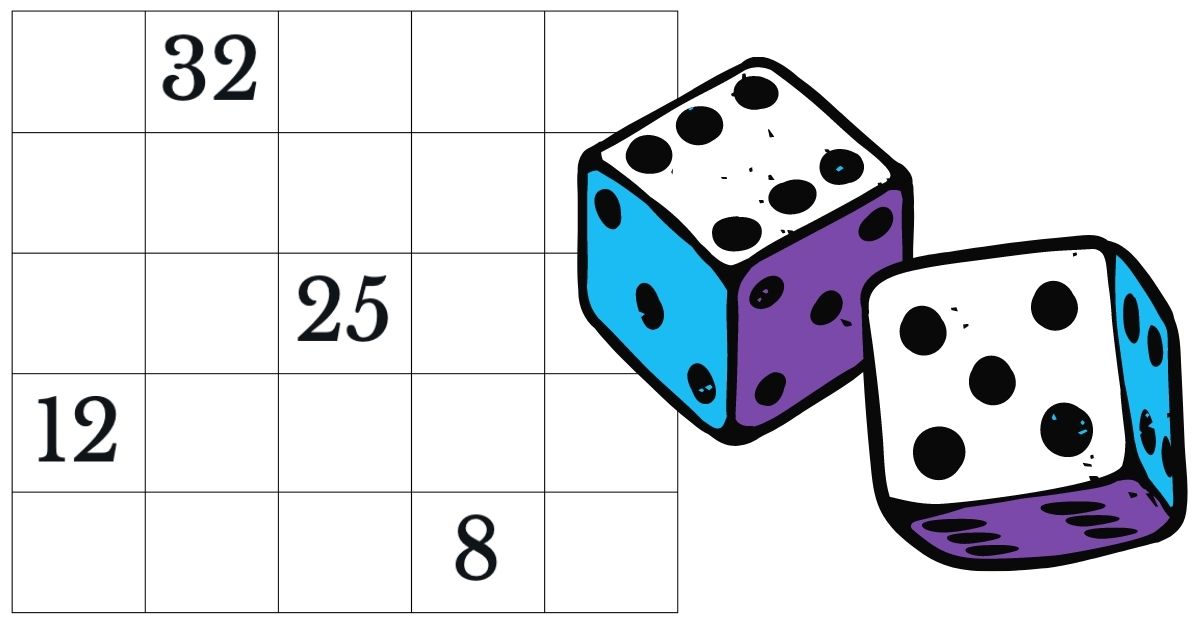
Nu började jag slå tärningarna och eleverna fick fundera vilken produkten av vad tärningarna visade var och sedan kryssa. Här kunde jag tydligt se vilka som hade börjat automatisera multiplikationstabellerna, vilka som förstod multiplikation men inte har påbörjat automatisering och även upptäcka de som inte förstod. Som vanligt i en årskurs fyra finns några tävlingsmänniskor och hettan stiger en aning när någon får tre eller fyra kryss i rad. Här upptäckte några elever att det tal som saknas inte går att få med hjälp av tärningarna (t ex 33, 11, 19). Vi lyckades i alla fall spela färdigt omgången då en elev till sist fick bingo.
Det faktum att vissa tal inte gick att få skapade nyfikenhet hos eleverna vilket i sin tur skapade en diskussion kring hur många av talen mellan 1-36 som inte kan kombineras med hjälp av tärningarna och varför. Vi gick gemensamt genom samtliga tal mellan 1 och 36. Eleverna fick fundera om de återfanns i någon multiplikationstabell och om de var möjliga att få med hjälp av tärningarna.
Efter detta fick återigen eleverna rita en bingobricka och fylla den med tal mellan 1-36. Några av eleverna förstod att de i de 25 rutorna måste placera tal som inte kunde bli en produkt av tärningsprickarna och att det gällde att placera dem strategiskt. Skulle de läggas i mitten, vid en kant, i ett hörn eller på olika ställen? Varför? Några elever motiverade sina placeringar muntligt i klassen. Därefter genomförde vi ytterligare ett bingospel. Innan våra 40 minuter var slut påpekade någon elev att vi borde spela någon gång med tiosidiga tärningar. Något jag tyckte var intressant med lektionen var att den nästan utan insats leder in elevernas nyfikenhet på frågan om varför vissa tal inte dök upp som produkter? Eleverna kommer då in på andra multiplikationstabeller som t ex 4×8 för talet 32 (vilket inte kunde skapas med tärningarna) men också bibehåller nyfikenheten kring tal som 11 och 31.
Lärarens tankar efter lektionen
Något jag tänker att man skulle kunna prova i lämplig grupp är att genomföra övningen med tiosidiga tärningar där bingobrickan är en hundraruta (där talen är slumpmässigt placerade) så kan eleverna diskutera egenskaperna hos de tal som förblir “okryssade”.
Lgr22 Syfte
Utveckla förmåga att formulera och lösa problem med hjälp av matematik och värdera valda strategier.
Centralt innehåll*
Formulering av matematiska frågeställningar utifrån vardagliga situationer.
Betygskriterier*
Eleven löser komplexa problem. Eleven ger förslag på alternativa tillvägagångssätt och värderar resultatens rimlighet.
Eleven för och följer matematiska resonemang genom att framföra och bemöta påståenden med väl underbyggda matematiska argument.
* årskurs 4-6

Min lärare på mellanstadiet introducerade Mattebingo i 4:an – och jag tror ingen i klassen någonsin tröttnade. Men framför allt: multiplikationstabellen upp till 15*15
sitter fortfarande i ryggmärgen efter 35 år. Hur kunde jag ”glömma”…….???