Årskurs 1-3
Matematik
Föregående tips Nästa tipsKor på bete – area och omkrets
Syfte
Eleverna ska förstå att arean är konstant även om man ändrar formen på ytan, men att omkretsen däremot förändras. En kvadrat har minst omkrets (i denna uppgift med de förutsättningar som föreligger). Eleverna får även träna på att föra och följa matematiska resonemang samt att samtala om, och argumentera för, olika lösningar.
Läraren reflekterar
Den här typen av uppgift engagerar ofta och leder in på sidospår som utvecklar både den ursprungliga idén och elevernas tankar och förståelse för matematiken. Det gäller att vara lyhörd för de sidospåren och lyfta in elevernas idéer i undervisningen. Det blir dessutom roligare!
Uppgift och upplägg
Eleverna får 16 ”gräsbitar” var (1*1 dm stora, gröna kartongbitar) och tre kor. De tre korna ska få lite olika hagar.
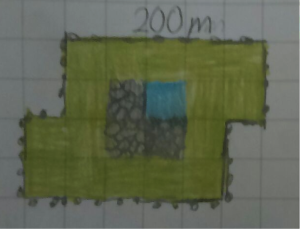
Ko nr 1 får själv bestämma hur hagen ska se ut. Förutom de 16 ”gräsbitarna” kan det finnas extra ytor med till exempel en damm eller å inne i hagen. Här gäller det att tänka ”utanför boxen”. Vad vill kon helst göra – springa runt, stå under en ek, hoppa över stenar, plaska i en damm…
Hagen ritas upp på cm-rutat papper. Hur stor är hagens ytteromkrets om en ”gräsruta” är 10*10 meter i verkligheten?

Eleverna placerade ut våra multibas-tiotal som staket runt hagen för att underlätta uträkningen, men det går ju lika bra med andra liknande trästavar. Gör man mindre kartongbitar kan tandpetare fungera bra som staket.
Ko nr 2 har en väldigt sparsam bonde som vill köpa så lite staket som möjligt. Vilken form får den kohagen och hur mycket staket går åt?

Ko nr 3 har en väldigt slösaktig bonde som älskar att sätta upp staket. Omkretsen ska alltså vara så stor som möjligt. Vilken form får den hagen? Eleverna fick redovisa sina tankar och funderingar för klassen. Får och nackdelar med olika hagar?
Fundera vidare
En möjlig fortsättning och utmaning kan vara att fundera på vilken form som ger störst area i förhållande till staketets omkrets (av till exempel kvadrat, femhörning, sexhörning, åttahörning och cirkel). Hur ska bonden bygga sitt staket så att det både blir stort och billigt?!
Lgr22 Syfte
Utveckla förmåga att formulera och lösa problem med hjälp av matematik och värdera valda strategier.
Centralt innehåll*
Grundläggande geometriska tvådimensionella objekt samt objekten klot, kon, cylinder och rätblock. Egenskaper hos dessa objekt och deras inbördes relationer. Konstruktion av geometriska objekt.
Jämförelser och uppskattningar av storheter. Mätning av längd, massa, volym och tid med vanliga nutida och äldre måttenheter.
Skala vid enkel förminskning och förstoring.
Formulering av matematiska frågeställningar utifrån vardagliga situationer.
Kriterier för bedömning av kunskaper*
Eleven använder och beskriver geometriska mönster och mönster i talföljder. Dessutom använder eleven grundläggande geometriska begrepp och vanliga lägesord för att beskriva geometriska objekts egenskaper, läge och inbördes relationer. Eleven använder och ger exempel på enkla proportionella samband.
Eleven avbildar och, utifrån instruktioner, konstruerar enkla geometriska objekt. Eleven gör enkla mätningar, jämförelser och uppskattningar av längder, massor, volymer och tider och använder vanliga måttenheter. Vid olika undersökningar avläser och skapar eleven enkla tabeller och diagram för att sortera och redovisa resultat.
* årskurs 1-3

Den här uppgiften använde jag till mina gamla elever när de gick i 6an läsåret 2016-2017. Det var en mycket rolig och uppskattad uppgift. Vi hade dock inte tiostavar att tillgå, utan använde oss av kaplastavar. Tiostavar tordes vara enklare.
Hej Sofie!
Jag funderar på att använda uppgiften i en liten undersökning och därför undrar jag om du har kommit på uppgiften själv eller om du har hittat/fått inspiration till det i någon bok?
Med hälsningar
Terje
Hej! Jag minns faktiskt inte om jag fått grundidén med kor och bete från någon annan (ev gammalt nationellt prov men väldigt osäker). Texten med snål bonde osv har jag kommit på själv vad jag vet. Även idén om att använda verkliga ”gräsbitar”, staket och kor är min egen.
Tack för ditt svar! Det ska bli spännande att testa uppgiften med eleverna!